Generacija harmonika višeg reda u nehomogenom polju

Članovi naučno-istraživačke grupe SAMOPHYS mr. Benjamin Fetić, mr. Kenan Kalajdžić i prof. dr. Dejan Milošević objavili su rad u specijalnom izdanju njemačkog naučnog časopisa Annalen der Physik posvećenom temi Ultrabrzi fenomeni na nanoskali (Ultrafast Phenomena at the Nanoscale) pod naslovom High-order harmonic generation by spatially inhomogeneous field (Generacija harmonika višeg reda u prostorno nehomogenom polju) u kojem je teorijski razmatran proces generacije harmonika višeg reda u nehomogenom polju koji se javlja u prisustvu metalnih nanostruktura.

1. Generacija harmonika višeg reda i nanostrukture

Međudjelovanje atomskih i molekularnih sistema sa jakim laserskim poljima manifestuje se u nizu fizikalnih pojava kao što su generacija harmonika višeg reda, jonizacija iznad praga, jonizacija iznad praga višeg reda, nesekvencijalna dvostruka jonizacija, i dr. Više o ovim procesima možete pročitati ovdje.

Ukratko, generacija harmonika višeg rada (HHG – High-order harmonic generation) može se opisati pomoću tzv. modela Tri koraka (eng. Three-step model) [1] prema kojem se u prvom koraku atom (molekula) jonizuje pod uticajem jakog laserskog polja. Zatim se oslobođeni elektron u drugom koraku ubrzava laserskim poljem koje ga u jednom trenutku vraća matičnom jonu. Konačno, u trećem koraku u procesu rekombinacije emituje se foton energije koja je jednaka neparnom umnošku energije fotona laserskog polja. Maksimalna energije fotona je određena formulom:

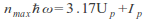
gdje su I_p energija jonizacije atoma, U_p ponderomotorna energija elektrona, a n redni broj emitovanog harmonika.

HHG je karakterstična pojava koja nastaje kao posljedica međudjelovanja atomskih i molekularnih sistema sa laserskim poljem i predstavlja obećavajući metod za dobijanje koherentnog ultravioletnog zračenja koje se može koristi u mnogim granama nauke. Međutim, prag za odvijanje generacije harmonika jeste da je intenzitet primijenjenog laserskog polja reda veličine 10¹⁴ Wcm^-2. Sa stanovišta tehnologije ostvarivanje ovako visokiih intenziteta lasera je veoma skup i zahtjevan zadatak.

Eksperimenti sa metalnim nanostrukturama pokazuju da je ovaj intenzitet moguće postići i sa laserikim poljima znatno nižeg intenziteta, reda veličine 10¹¹ Wcm^-2 tako što se iskoristi lokalno plazmonsko rezonantno pojačavanje polja u blizini nanostruktura. U radu iz 2008. godine [2] južnokorejski naučnici su iskoristili upravo ovaj proces za dobijanje harmonika višeg reda. U eksperimentu je korišten femtosekundni laserski puls pomoću kojeg se djeluje na safirni substrat na kojem su formirane zlatne nanostrukture u obliku leptir kravate (eng. Bow-tie shape). Usljed međudjelovanja laserskog polja i slobodnih elektrona u slobodnom prostoru između nanostruktura dolazi do formiranja električnog polja čiji je intenzitet do tri reda veličine veći od intenziteta primijenjenog laserskog polja. Ovo lokalno plazmonsko polje je sasvim dovoljno jako za generaciju harmonika višeg reda. U prorez nanostruktura ubrizgava se snop atoma argona u gasovitom stanju i kao posljedica međudjelovanja lokalnog polja i atoma gasa dolazi do emisije harmonika višeg reda. Na slici 1 predstavljen je shematski prikaz eksperimenta.

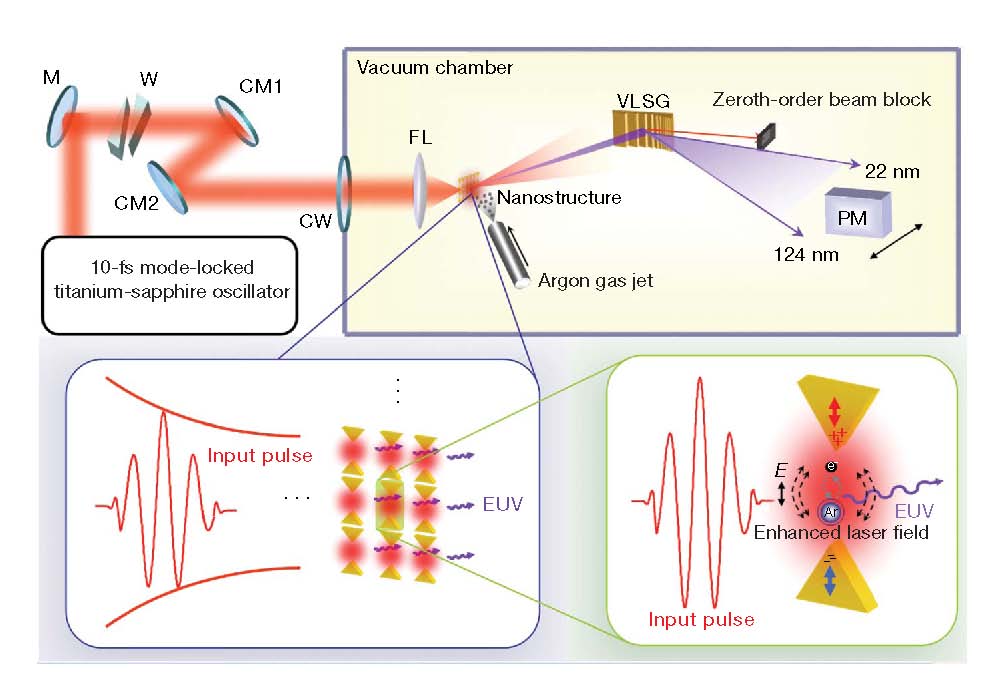
Slika 1. : Shematski prikaz dobijanja lokalnog plazmonskog polja pomoću “bow-tie” nanostruktura. U prostor između šiljaka nanostruktura ubacuje se mlaz atoma argona. Usljed interakcije sa lokalnim poljem, atomi argona se jonizuje. Elektron nakon jonizacije može da se vrati matičnom jonu. U procesu rekombinacije dolazi do emisije fotona čija je energija jednaka cjelobrojnom umnošku energije fotona laserskog polja.

2. Teorijsko opisivanje HHG-a u nehomogenom polju

U dosadašnjim teorijskim razmatranjima HHG procesa obično se podrazumijeva da je lasersko polje homogeno. U klasičnom modelu Tri koraka [1], elektron se “rodi” u kontinuumu u ishodištu koordinatnom sistemu sa početnom brzinom jednakom nuli. Zavisno od trenutka jonizacije elektron može da postigne energije u laserskom polju koje dostižu do 3.17U_p. Spektar viših harmonika se karakteriše platoom (područje u kojem je intenzitet harmonika približno konstantan) i cutoff-om (maksimalnom energijom harmonika nakon koje intenzitet naglo opada, tj. imamo “odsijecanje” – cutoff). Model Tri koraka ilustrativno je prikazan na slici 2. Zbog nehomogenosti polja očekujemo da elektronske trajektorije u laserskom polju budu modifikovane u odnosu na slučaj homogenog polja.

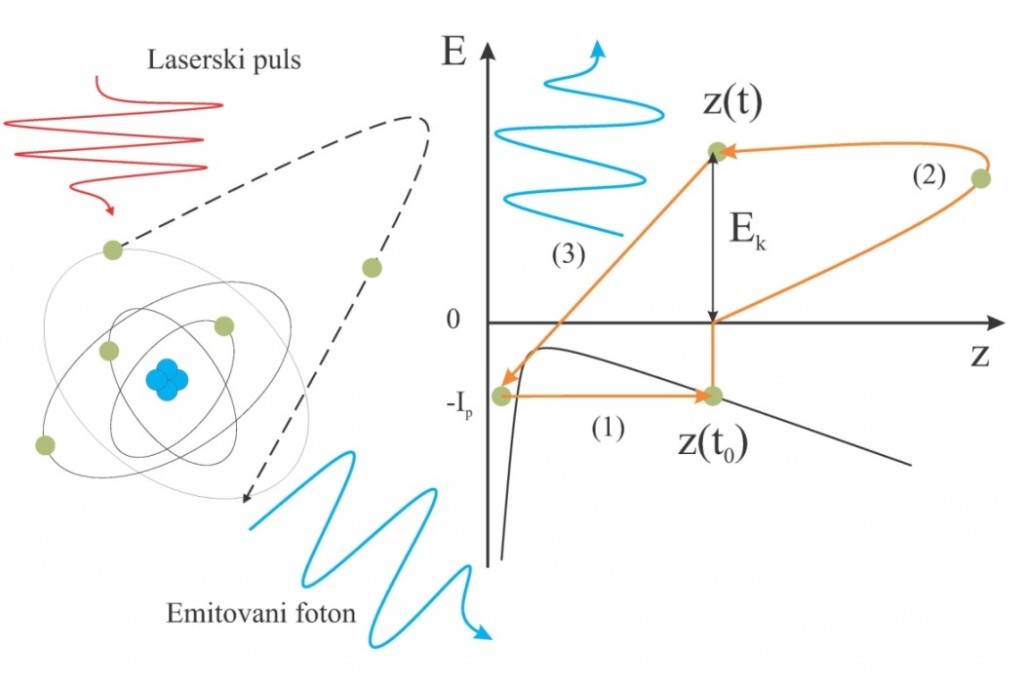
Slika 2. : Model Tri koraka. Lasersko polje jonizuje valentni electron. Elektron se rodi u kontinuumu u tački z(t₀). Pod uticajem laserskog polja elektron nakon određenog vremena može da se vrati matičnom jonu. U procesu rekombinacije emituje se foton.

Ako se nehomogeno električno polje simulira vremenski i prostorno promjenljivom funkcijom

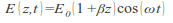
tada numeričko rješavanje vremenski zavisne Schrödingerove jednačine (time – dependent Schrödinger equation – TDSE) pokazuje da nehomogenost polja može znatno da produži plato, odnosno položaj cutoff – a u spektru viših harmonika [3, 4, 5]. To znači da je maksimalna energija emitovanog fotona znatno veća od energije koja je data formulom (1). Na slici 3 su prikazani spektri emitovanih harmonika za različite parametre nehomogenosti polja β i kao što možemo primijetiti, plato je znatno duži u odnosno plato za homogeno polje. U nehomogenom polju, elektron ubrzan laserskim poljem može da postigne znatno veće energije u odnosu na 3.17U_p. Zbog toga je za očekivati da imamo znatno produženi plato, dok se položaj cutoff – a pomjera ka viših energijama emitovanih fotona. S druge strane, zbog narušenja simetrije, u spektru se pojavljuju i parni harmonici.

Pored toga, s povećanjem dužine trajanja laserskog impulsa, u spektru se pojavljuje dodatni plato. Na desnom grafiku slike 3 prikazan je spektar za znatno duže laserske pulseve u trajanju od deset optičkih ciklusa. U zavisnosti od parametra nehomogenosti polja, pojavljuje se dodatni plato. Pojava dodatnog platoa ne može se objasniti primjenog modela Tri koraka pod uobičajenim pretpostavkama. Jednostavno rečeno, TDSE analiza pokazuje da je moguća emisija harmonika znatno viših frekvencija nego što to model Tri koraka predviđa.

U radu [3] je predstavljen modifikavani model Tri koraka koji uzima u obzir da elektron nakon tuneliranja kroz potencijalnu barijeru ima početnu brzinu koja je različita od nule kao i da mjesto pojave elektrona u koontinuumu nije u ishodištu koordinatnog sistema kao što se u modelu Tri koraka obično pretpostavlja. S obzirom da je prvi korak jonizacija iznad praga, početna brzina elektrona koji se “rodi” u kontinuumu je određena formulom

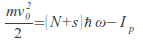
gdje je N najmanji broj fotona potreban za joniziaciju, dok s (s = 0, 1, 2, …) predstavlja dodatni broj apsorbovanih fotona.

Modifikovani model Tri koraka pokazuje da elektron može postići znatno veće energije. Pored toga, naš model pokazuje da se elektroni, koji u trenutku rekombinacije imaju energije koje odgovaraju dodatnom platou, jonizuju u trenutku kada je jačina polja znatno manja, pa je vjerovatnoća jonizacije za ove elektrone manja. Ova činjenica u spektru se manifestuje kao plato koji je dosta niži u odnosu na standardni plato.

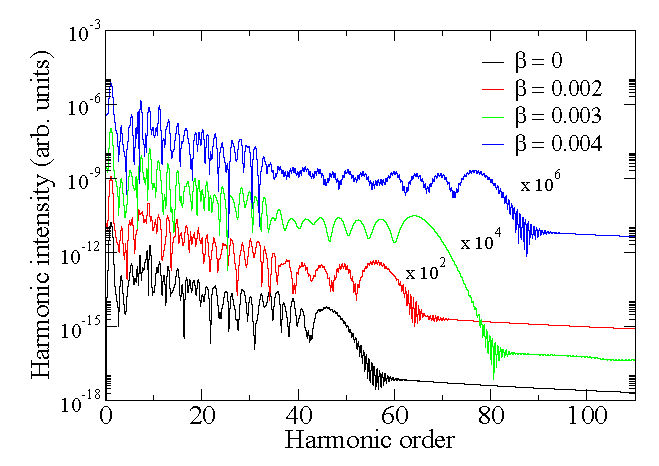
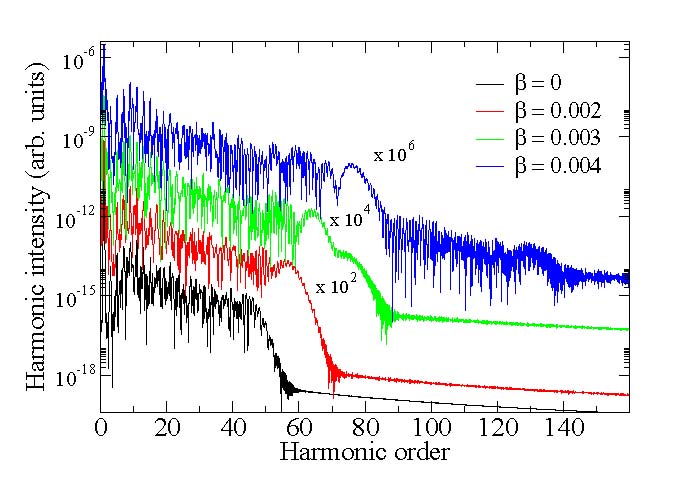
Slika 3: Intenzitet emitovanih harmonika u zavisnosti od parametra β nehomogenosti električnog polja. Predstavljeni spektri dobijeni su numeričkim rješavanjem TDSE. Možemo uočiti da se položaj cut-offa pomjera u područje većih frekvencija s povećanjem parametra β. Na lijevoj slici je predstavljen spektar viših harmonika za vrijeme trajanja laserskog pulsa od četiri optička ciklusa, dok je na desnoj slici predstavljen spektar za laserski puls u trajanju od deset optičkih ciklusa. Intenzitet laserskog pulsa je 3· 10¹⁴ W/cm^-2, a talasna dužina 800 nm.

Reference :

[1]  P. B. Corkum, Plasma perspective on strong field multiphoton ionization: Phys. Rev. Lett. 71, 1994 (1993).

[2] S. Kim, J. Jin, Y.-J. Kim, In-Y, Park, Y. Kim, and S.-W. Kim: High–order harmonic generation by resonant plasmon field enhancement, Nature 453, 757 – 760 (2008).

[3]  B. Fetić, K. Kalajdžić, and D. B. Milošević: High-order harmonic generation by spatially inhomogeneous field, Annalen der Physik (Berlin), 1-11 (2012).

[4]  I. Yavuz, E. A. Bleda, Z. Altun, and T. Topcu: Generation of broadband XUV continuum in high-order harmonic generation by spatially inhomogeneous fields, Phys. Rev. A 85, 013416 (2012).

[5] M.F. Ciappina, J. Biegert, R. Quidant, and M. Lewenstein: High-order harmonic generation from inhomogeneous fields, Phys. Rev. A 85, 033828 (2012).

• Prethodna
• Sljedeća