Atomski i molekularni procesi u jakom laserskom polju
Laseri predstavljaju jedan od najznačajnijih izuma dvadesetoga vijeka. Razvoj lasera je bio buran od samog njihovog otkrića 1960. godine. I danas, u 21. vijeku, tempo razvoja lasera i njihove primjene je izuzetno živ, tako da to područje nauke i tehnike predstavlja izazov za mlade istraživače.
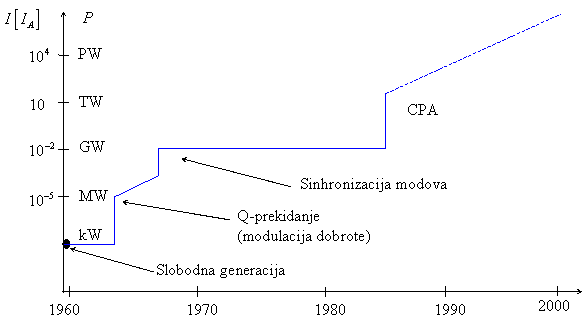
Slika 1: Razvoj lasera velikih snaga.
Na slici 1 je predstavljen razvoj lasera od njihovog otkrića do danas [1]. Na apscisi su prikazane godine, a na ordinatu su naneseni snaga P u vatima i intenzitet laserskog polja I koji se postiže ako se lasersko zračenje snage P fokusira na površinu S radijusa
Procesi koji se odvijaju u atomima, kao što su pobuđenje atoma, jonizacija itd. se mogu precizno opisati koristeći metode kvantne mehanike. Npr., primjenom Diracovog vremenski zavisnog računa perturbacije može se izvesti tzv. Fermijevo zlatno pravilo koje omogućava da se na jednostavan način izračunaju vjerovatnoće kvantno-mehaničkih procesa [3]. Za proces jonizacije atoma elektromagnetnim poljem energija upadnog fotona
Krajem 70-tih godina prošloga vijeka su prvi puta eksperimentalno zapaženi multifotonski procesi. 1977. godine Weingartshofer sa saradnicima [4] je zapazio da se pri rasijanju elektrona upadne energije
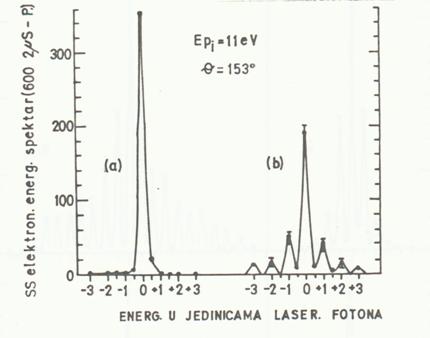
To znači da je u toku procesa rasijanja apsorbovano
Sa otkrićem tzv. ATI procesa (Above-Threshold-Ionization), tj. jonizacije iznad praga, 1979. godine [5], može se reći da je fizika atomskih procesa u laserskom polju ušla u neperturbativni režim. ATI spektar, tj. spektar kinetičkih energija fotoelektrona nastalih ozračavanjem atoma jakim laserskim poljem, sastoji se od serije maksimuma na međusobnom rastojanju jednakom energiji jednog fotona [slika 3; sa
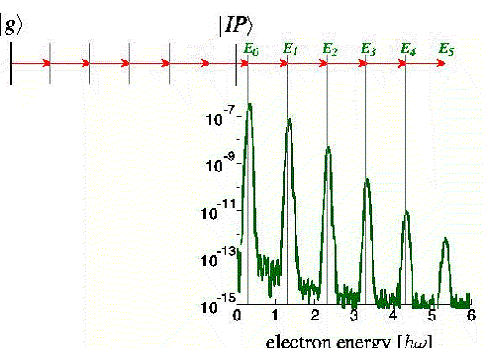
Slika 3: Spektar fotoelektrona u ATI režimu [6].
U drugoj polovini 1980-tih godina je otkriven još jedan interesantan atomski proces koji se odvija u prisustvu jakog laserskog polja: generacija viših harmonika (HHG: High-order Harmonic Generation) [7]. Kada se ultrakratki laserski impuls fokusira na gas u atomskom stanju, zapaža se generacija izuzetno velikog broja (više stotina) neparnih harmonika upadnog laserskog zračenja. Tipični spektar viših harmonika je predstavljen na slici 4. Nakon naglog pada efikasnosti emisije harmonika pri povećanju reda harmonika N, zapaža se oblast platoa u kojoj efikasnost emisije opada sporo sa povećanjem N. Za 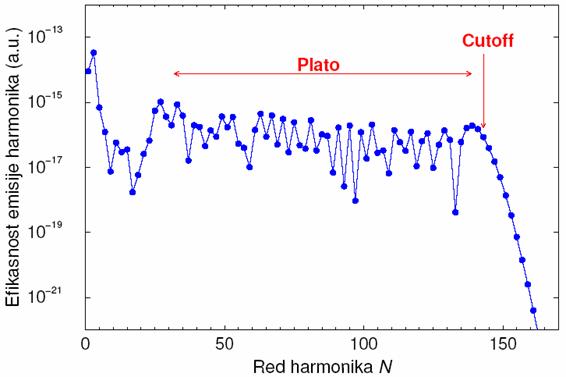
Slika 4: Efikasnost emisije harmonika kao funkcija reda harmonika N, za HHG atomima helijuma (![]() ) ozračenim linearno polarizovanim poljem Ti:S lasera talasne dužine 800 nm i intenziteta
) ozračenim linearno polarizovanim poljem Ti:S lasera talasne dužine 800 nm i intenziteta ![]() . Na slici je označeno područje platoa i cutoff. Teorijski rezultat za cutoff je
. Na slici je označeno područje platoa i cutoff. Teorijski rezultat za cutoff je ![]() .
.
Fizika mikrosvijeta se uspješno objašnjava kvantnom mehanikom. Newtonovi zakoni ne važe u svijetu atoma. Prvi pokušaji objašnjenja pojava u mikrosvijetu su se služili analogijama sa klasičnim sistemima. Npr., prema Bohrovom modelu atoma elektroni kruže oko jezgra po eliptičkim putanjama analogno kao planete oko Sunca. Tokom razvoja kvantne teorije takve klasične analogije su odbačene. Standardna matematička formulacija kvantne mehanike, koja čini osnovu za proračun procesa u mikrosvijetu, je gotovo potpuno u suprotnosti sa našom intuicijom baziranom na zakonima klasične fizike koji vrijede u makrosvijetu. Pa ipak, sa osnovnim pojmovima kvantne teorije, kao što su to talasna funkcija koja opisuje česticu i statistička interpretacija te funkcije, Heisenbergov princip neodređenosti itd., danas se već upoznaju i srednjoškolci. Postoji i alternativna formulacija kvantne mehanike koja je mnogo bliža klasičnim konceptima. Ona se bazira na metodu integrala po putanjama (trajektorijama) koji je razvio Feynman [8]. Prema Feynmanovoj formulaciji, amplituda vjerovatnoće M nekog kvantno-mehaničkog procesa se može predstaviti kao koherentna superpozicija doprinosa svih mogućih prostorno-vremenskih putanja koje povezuju početno i konačno stanje sistema. Svaki od tih doprinosa predstavljen je kompleksnim brojem čija je faza jednaka klasičnoj akciji [9] duž te putanje:
Nedavno je otkriveno da se primjenom metoda integrala po putanjama mogu riješiti problemi fizike interakcije jakog [10] laserskog polja i atoma. Primjeri takvih procesa su jonizacija iznad praga višeg reda (HATI – High-order ATI) i generacija viših harmonika (HHG). U HATI procesu atom može da apsorbuje na stotine fotona više nego što je to neophodno da bi došlo do jonizacije, tako da se u tom procesu emituju elektroni velikih energija. Frekvencija emitovanog zračenja u HHG procesu je jednaka cjelobrojnom umnošku frekvencije upadnog laserskog zračenja koje se fokusira na sredinu (najčešće gas). U eksperimentima je zapaženo zračenje frekvencije i do 300 puta veće od frekvencije fundamentalnog harmonika
Ovi teorijski rezultati su potvrđeni nizom eksperimenata izvršenih u Max-Planck-Institutu za kvantnu optiku u Garchingu kod Münchena (HATI) i u Saclayu kod Parisa (HHG). Ovdje nemamo namjeru ulaziti u detalje tih eksperimenata i teorije koja ih objašnjava [12]. Umjesto toga, kao ilustracija, na slici 5 je predstavljen HATI spektar atoma ksenona ozračenih eliptički polarizovanim laserskim poljem. Detektovani elektroni su emitovani pod uglom od
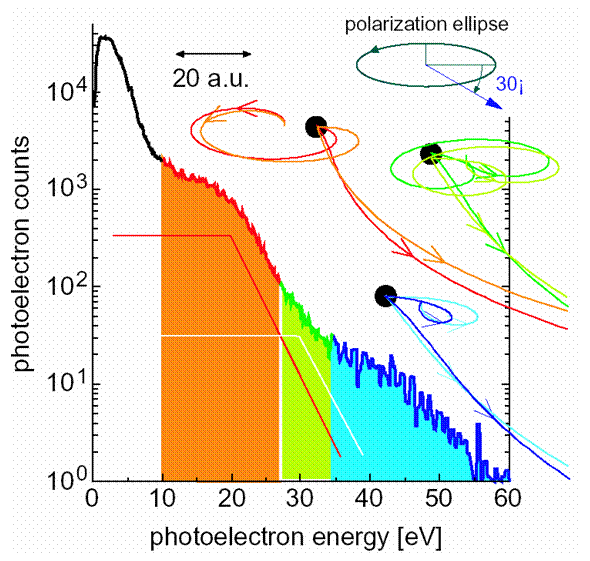
Napredak laserske tehnologije početkom 21. vijeka je omogućio stvaranje veoma kratkih laserskih impulsa velikih snaga [13,14]. Dužina trajanja ovakvih impulsa iznosi svega nekoliko optičkih ciklusa, a njihova snaga se mjeri teravatima. Jačina tako nastalog laserskog polja nerijetko prelazi jačinu elektrostatičkog polja u atomu. Stoga interakcija ultrakratkih laserskih impulsa sa materijom može poslužiti za ispitivanje dinamike atomskih i unutar-molekularnih procesa, s jedne strane, i određivanje karakteristika samog laserskog zračenja, s druge strane.
Laserski sistemi mogu da emituju lasersko zračenje kontinuirano ili u kratkim impulsima. Kontinuirani režim rada lasera podrazumijeva emisiju svjetlosti bez prekida od trenutka uključivanja lasera pa sve do njegovog isključenja. Kod impulsnog režima svjetlost se emituje u tačno određenim vremenskim intervalima jednom ili više puta. Ultrakratki laserski impuls podrazumijeva zračenje čiji je trajanje reda veličine jedne femtosekunde (1fs = 10-15 s) [14].
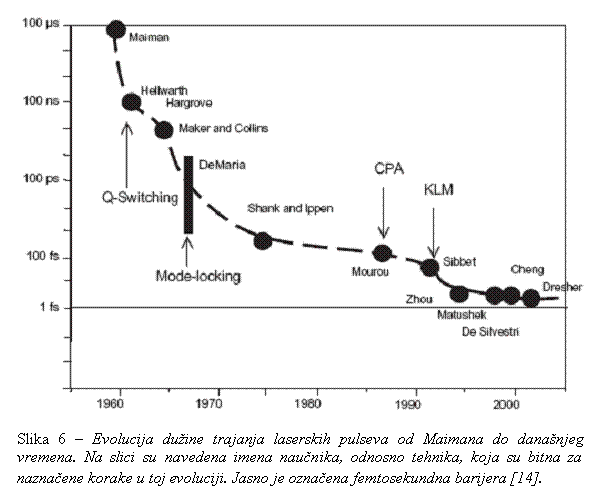
Mjerenje kratkih vremenskih intervala je neodvojivi dio procesa dobijanja informacija o dinamici fizikalnih procesa. Na sličan način kao što smo na slici 1 predstavili razvoj lasera prateći povećanje ostvarenog maksimalnog intenziteta, tako možemo predstaviti i istorijski progres tehnologija ostvarivanja ultrakratkih laserskih impulsa (slika 6). Vrijeme trajanja impulsa prvih impulsnih lasera (Maiman, 1960. godine) je bilo nekoliko stotina mikrosekundi. U toku nekoliko narednih godina napredak je bio vrlo brz. Pronalazak Q-prekidača (Hellwarth, 1961. godine) je smanjio dužinu impulsa na 10 ns, a otkriće metode sinhronizacije modova (DeMaria sa saradnicima, 1966. godine) i lasera na bazi boja (Shank i Ippen, 1974. godine) ju je spustio ispod jedne pikosekunde. Kao i u slučaju razvoja lasera velikih snaga, krajem sedamdesetih i početkom osamdesetih godina dvadesetog vijeka je došlo do zastoja. Znatnije skraćenje laserskih impulsa je ostvareno tek za 15-tak godina. Sredinom osamdesetih godina najkraći ostvareni impulsi sa laserima na bazi boja bili su oko 6 fs, a razvoj CPA tehnike je omogućio laserske impulse dužine trajanja svega nekoliko optičkih ciklusa (tzv. few-cycle pulses; 5 fs za Ti:S laser na 800 nm). S obzirom da jedan optički ciklus koji odgovara talasnoj dužini Ti:S lasera iznosi 2,7 fs, jasno je da se, da bi se probila femtosekundna barijera označena na slici 6, moraju koristiti kraće talasne dužine, odnosno veće energije fotona. Probijanje te barijere je povezano sa napretkom u proučavanju atomskih procesa u jakom laserskom polju. Razvijena je potpuno nova oblast nauke koja je nazvana atonauka (attoscience).
Da bi se mogla proučavati interakcija elektromagnetnog zračenja i materije neophodno je poznavati kako se elektromagnetno polje mijenja u prostoru i vremenu. Impuls linearno polarizovanog laserskog zračenja čija je vrijeme trajanja znatno veće od jednog optičkog perioda potpuno je okarakterisan frekvencijom i intenzitetom zračenja. Za impulse koji traju nekoliko optičkih ciklusa potrebno je pored ovih parametara poznavati još dvije veličine: ukupno vrijeme trajanja impulsa Tp i tzv. CE fazu ili apsolutnu fazu ![]() (carrier wave-envelope relative phase – relativna faza između nosećeg talasa frekvencije i obvojnice). Da bismo ovo bolje objasnili, vremensku zavisnost vektora jačine linearno polarizovanog električnog polja lasera predstavimo u obliku:
(carrier wave-envelope relative phase – relativna faza između nosećeg talasa frekvencije i obvojnice). Da bismo ovo bolje objasnili, vremensku zavisnost vektora jačine linearno polarizovanog električnog polja lasera predstavimo u obliku: ![]() . Amplituda
. Amplituda ![]() zavisi od vremena i njezin oblik se može eksperimentalno ustanoviti. Za analitičko opisivanje ove zavisnosti se može npr. koristiti slijedeća zavisnost:
zavisi od vremena i njezin oblik se može eksperimentalno ustanoviti. Za analitičko opisivanje ove zavisnosti se može npr. koristiti slijedeća zavisnost: ![]() . Na slici 7 je prikazana vremenska zavisnost vektora
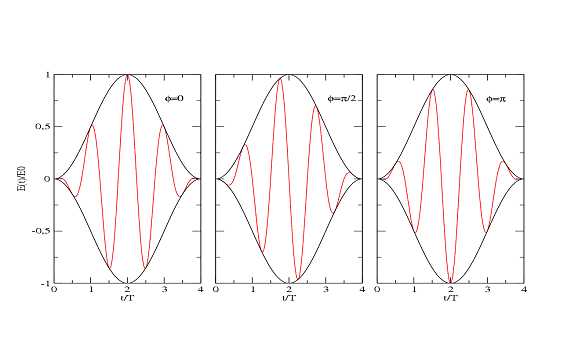
. Na slici 7 je prikazana vremenska zavisnost vektora ![]() i amplitude (obvojnice) za različite vrijednosti parametra
i amplitude (obvojnice) za različite vrijednosti parametra ![]() . Položaj maksimalne vrijednost jačine električnog polja u odnosu na vrh obvojnice se mijenja sa promjenom CE faze. Za impulse znatno duže od perioda električnog polja uticaj ove veličine nije veliki, jer će vremenski trenutak u kome električno polje ima maksimalnu vrijednost uvijek biti blizu vrha obvojnice. Međutim, za ultrakratke impulse uticaj CE faze postaje značajan. Pri interakciji ultrakratkog laserskog polja i atoma ili molekula, svi procesi koji zavise od vektora jačine električnog polja zavisit će i od CE faze. Zbog toga su mjerenje i stabilizacija CE faze jako bitni za ove procese. Efekti CE faze su prvi put eksperimentalno dokazani 2001. godine [15], a naredne godine su ti rezultati objašnjeni teorijski [16].
. Položaj maksimalne vrijednost jačine električnog polja u odnosu na vrh obvojnice se mijenja sa promjenom CE faze. Za impulse znatno duže od perioda električnog polja uticaj ove veličine nije veliki, jer će vremenski trenutak u kome električno polje ima maksimalnu vrijednost uvijek biti blizu vrha obvojnice. Međutim, za ultrakratke impulse uticaj CE faze postaje značajan. Pri interakciji ultrakratkog laserskog polja i atoma ili molekula, svi procesi koji zavise od vektora jačine električnog polja zavisit će i od CE faze. Zbog toga su mjerenje i stabilizacija CE faze jako bitni za ove procese. Efekti CE faze su prvi put eksperimentalno dokazani 2001. godine [15], a naredne godine su ti rezultati objašnjeni teorijski [16].
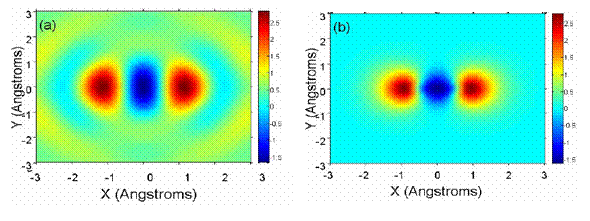
Kao što je pomenuto u prethodnom odjeljku, ostvarenje impulsa kraćih od 1 fs je dovelo do razvoja nove oblasti nauke za koju je usvojen naziv atofizika (attophysics). Atofizika je prirodan nastavak femtohemije (A. Zewail je 1999. godine dobio Nobelovu nagradu za hemiju za svoja otkrića u toj oblasti). Najnovija dostignuća naše grupe su upravo vezana za atofiziku. Primjenom otkrića u toj oblasti fizike je moguće analizirati strukturu molekula i dinamiku atomskih i molekularnih procesa. Npr., jedna od primjena atofizike je tomografija molekularnih orbitala [17] pomoću koje “vidimo” i amplitudu i fazu elektrona u molekuli. To se postiže tako što se pri rotaciji molekula snima spektar viših harmonika. Zatim se iz eksperimentalnih podataka matematički izračunava talasna funkcija osnovnog stanja (slika 8).
Očekuje se da će dalji razvoj ove oblasti fizike biti buran. Kao ilustracija, na slici 9 je šematski prikazan predviđeni razvoj u ostvarivanju maksimalnih intenziteta laserskog polja i novi vidici koji se time otvaraju. Naučnici sa Univerziteta u Michiganu su u aprilu 2008. godine pomoću Hercules lasera postigli trenutni rekord u maksimalnoj snazi – 300 TW. Fokusiranjem pulseva dužine trajanja 30 fs ostvarili su rekordni intenzitet od ![]() .
.
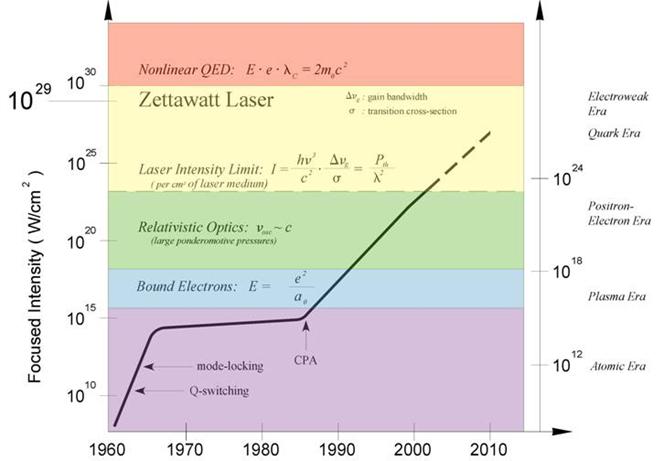
Slika 9: Predviđanja daljeg razvoja fizike interakcije ultrajakog elektromagnetnog polja i materije.
Korisni linkovi:
Non-linear Optics - Institute of Optics and Quantum Electronics Jena
Agostini - DiMauro Atomic Physics Research GroupAtomic and Plasma Physics
Attophysics
The Institute of Photonic Sciences
Laser Physics Web Site
Quantum Dynamics and Attosecond Physics
Arxiv
IOP Insitute of Physics
Encyclopedia of Laser Physics and Technology
Web stranica Gerhard G.Paulas
Imperial Collegue -Quantum Optics and Laser Science
Reference
[1] Dejan Milošević, Osnove lasera (sa zbirkom riješenih zadataka), Sarajevo, 1996.>
[2] D. Strickland, G. Mourou, Opt. Commun. 56, 216 (1985); M. Perry, G. Mourou, Science 264, 917 (1994).
[3] W. Greiner, Quantum mechanics. An introduction, Springer, Berlin, 1989.
[4] A. Weingartshofer, J. K. Holmes, G. Caudle, E. M. Clarke, H. Kruger, Phys. Rev. Lett. 39, 269 (1977).
[5] P. Agostini, F. Fabre, G. Mainfray, G. Petite, N. K. Rahman, Phys. Rev. Lett. 42, 1127 (1979).
[6] W. Becker, F. Grasbon, R. Kopold, D. B. Milošević, G. G. Paulus, H. Walther, “Above-threshold ionization: From classical features to quantum effects”, Advances in Atomic, Molecular, and Optical Physics 48, 35-97, Academic Press, Boston (2002).
[7] A. McPherson, G. Gibson, H. Jara, U. Johann, T. S. Luk, I. A. McIntyre, K. Boyer, C. K. Rhodes, J. Opt. Soc. Am. B 4, 595 (1987); M. Ferray, A. l'Huillier, X. F. Li, L. A. Lompré, G. Mainfray, C. Manus, J. Phys. B 21, L31 (1988).
[8] R. P. Feynman, A. R. Hibbs, Quantum mechanics and path integrals, McGraw-Hill, New York, 1965.
[9] Akcija za vremenski interval od trenutka ![]() do trenutka
do trenutka ![]() se definiše kao
se definiše kao ![]() ,
, ![]() , gdje je L Lagrangeova funkcija, T kinetička energija, a V potencijalna energija. Od svih mogućih putanja klasičnom kretanju odgovara ona za koju je akcija minimalna. To je tzv. princip najmanje akcije koji omogućava da se odrede klasične jednačine kretanja.
, gdje je L Lagrangeova funkcija, T kinetička energija, a V potencijalna energija. Od svih mogućih putanja klasičnom kretanju odgovara ona za koju je akcija minimalna. To je tzv. princip najmanje akcije koji omogućava da se odrede klasične jednačine kretanja.
[10] Jačina laserskog polja dostiže jačinu Coulombovog polja koje elektron osjeća u atomu, tako da se uticaj laserskog polja na atomske procese više ne može smatrati malom perturbacijom, tj. proces je izrazito nelinearan po laserskom polju.
[11] R. Kopold, D. B. Milošević, W. Becker, “Rescattering processes for elliptical polarization: a quantum trajectory analysis”, Phys. Rev. Lett. 84, 3831 (2000).
D. B. Milošević, “Cut-off law for high-harmonic generation by an elliptically polarized laser field”, J. Phys. B 33, 2479 (2000).
[12] P. Salières, B. Carré, L. Le Dérof, F. Grasbon, G. G. Paulus, H. Walther, R. Kopold, W. Becker, D. B. Milošević, A. Sanpera, M. Lewenstein, “Feynman's path-integral approach for intense-laser-atom interactions”, Science 292, 902 (2001). Ovaj rad je uvršten u rubriku “News of the weak” časopisa Science, str. 823, uz odgovarajući komentar. Članak o tome radu objavljen je i u dnevnom listu Frankfurter Algemaine Zeitung od 30. maja 2001. godine pod naslovom: “Die Pfade des eingefangenen Lichts”.
[13] Elvedin Hasović, “Jonizacija ultrakratkim laserskim poljem”, diplomski rad, Prirodno-matematički fakultet Univerziteta u Sarajevu, decembar 2004.
[14] P. Agostini, L. F. DiMauro, “The physics of attosecond light pulses”, Rep. Prog. Phys. 67, 813-855 (2004).
[15] G. G. Paulus, F. Grabson, H. Walther, P. Villoresi, M. Nisoli, E. Priori, S. Stagira, S. De Silvestri, “Absolute-phase phenomena in photoionization with few-cycle laser pulses”, Nature 414, 182 (2001).
[16] D. B. Milošević, G. G. Paulus, W. Becker, “Phase dependent effects of a few-cycle laser pulse”, Phys. Rev. Lett. 89, 153001 (2002).
[17] J. Itatani, J. Levesque, D. Zeidler, H. Niikura, H. Pepin, J. C. Kieffer, P. B. Corkum, D. M. Villeneuve, Tomographic imaging of molecular orbitals , Nature 432, 867 (2004).


