Generacija atosekundnih pulseva pomoću ortogonalnih bihromatskih laserskih polja

Dana 18.10.2021. godine objavljen je rad pod naslovom “Attosecond pulse trains with elliptical polarization from an orthogonally polarized two-color field” u američkom časopisu Journal of the Optical Society of America B. Autori rada su dr. Dino Habibović i akademik prof. dr. Dejan Milošević sa Odsjeka za fiziku Prirodno-matematičkog fakulteta Univerziteta u Sarajevu i prof. dr. Wilhelm Becker sa Max Born instituta u Berlinu.

U objavljenom radu autori analiziraju mogućnost generisanja atosekundnih pulseva generacijom harmonika višeg reda (HHG) pomoću ortogonalnog bihromatskog laserskog polja (OTC). Ovi pulsevi su od velike važnosti za ispitivanje različitih fizičkih, hemijskih i bioloških procesa koji se odvijaju na subfemtosekundnoj skali (1 femtosekunda = 10^-15 s). Jedan način za generisanje ovakvih pulseva podrazumijeva korištenje ultrakratkih laserskih snopova (tzv. few-cycle laseri) čije je vrijeme trajanja pulsa toliko kratko da obuhvata svega nekoliko optičkih ciklusa. Drugi način za dobijanje atosekundnih pulseva je baziran na tzv. ‘polarization-gate’ tehnici koja je zasnovana na činjenici da je vjerovatnoća emisije harmonika veoma osjetljiva na elipticitet laserskog pulsa, tj. naglo opada sa porastom elipticiteta. Stoga je 1994. godine Corkum predložio korištenje laserskog snopa sa vremenski-zavisnim elipticitetom za generisanje atosekundnih pulseva. Kasnije su razvijene brojne druge metode za generisanje ultrakratkih pulseva kao što je metoda zasnovana na korištenju dva kružno polarizovana polja od kojih je jedno few-cycle, dok je drugo dugo lasersko polje, ili pak metoda koja koristi kružno polarizovani snop zajedno sa koplanarnim statičkim laserskim poljem.

Za generisanje viših harmonika koristili smo atome plemenitih gasova i OTC polje. Ovo polje se sastoji od dvije linearno polarizovane komponente sa frekvencijama koje su cjelobrojni umnošci određene frekvencije (tzv. fundamentalna frekvencija) i međusobno okomitim polarizacijama. Osnovna prednost ove šeme u odnosu na druge šeme koje uključuju dvokomponentna polja je da omogućava generisanje eliptički polarizovanih harmonika. Ovi harmonici dalje mogu poslužiti za generisanje eliptički polarizovanih atosekundnih pulseva. Dodatno, za razliku od bicirkularnog polja, koje se sastoji od dvije kružno polarizovane komponente i koje takođe omogućava generisanje eliptički polarizovanih atosekundnih pulseva, OTC polje podržava generaciju harmonika sa većim energijama i značajnom vjerovatnoćom emisije. Takođe, relativna faza između komponenata laserskog polja može poslužiti kao kontrolni parametar, tj. vjerovatnoća emisije viših harmonika i njihov elipticitet jako zavise od vrijednosti relativne faze. Ovaj parametar ne utječe na spektar generisan bicirkularnim laserskim poljem.

U objavljenom radu smo koristili OTC lasersko polje sa frekvencijama koje su neparni umnošci fundamentalne frekvencije koja odgovara talasnoj dužini od 1300 nm. Za ovakvu kombinaciju frekvencija emitovani harmonici su eliptički polarizovani. Osnovni cilj ovoga rada je da ispita da li je moguće, sa ovakvim OTC poljem, generisati više harmonika pogodne za generaciju eliptički polarizovanog atosekundnog pulsa. Harmonici u odabranoj grupi trebaju biti eliptički polarizovani i fazno-usaglašeni. Fazno-usaglašeni harmonici odgovaraju glatkim dijelovima spektra, tj. dijelovima spektra gdje se vjerovatnoća emisije sporo mijenja kao funkcija reda harmonika. Kao mjeru fazne usaglašenosti koristili smo odnos R koherentne i nekoherentne sume električnih polja odabrane grupe harmonika. Rezultati numeričkih simulacija su pokazali da je, ukoliko upotrijebimo helijum kao metu, elipticitet harmonika koji odgovaraju glatkim dijelovima spektra mali, pa je i odgovarajući atosekundni puls približno linearno polarizovan. Na lijevim panelima slike se vidi da je elipticitet emitovanih harmonika koji odgovaraju glatkim dijelovima spektra (tj. koji su fazno-usaglašeni) mali nezavisno od vrijednosti relativne faze (pogledati crvenu tačkastu i zelenu isprekidanu liniju). Sa druge strane, situacija je drugačija ukoliko kao metu koristimo atome neona. Odgovarajući rezultati za intenzitet emisije i elipticitet emitovanih harmonika kao funkcije reda harmonika su predstavljeni na gornjem i donjem desnom panelu, respektivno. Posebno je interesantno područje koje odgovara redovima harmonika od n = 59 do n = 151 za relativnu fazu u iznosu od 60 stepeni (zelena isprekidana linija).

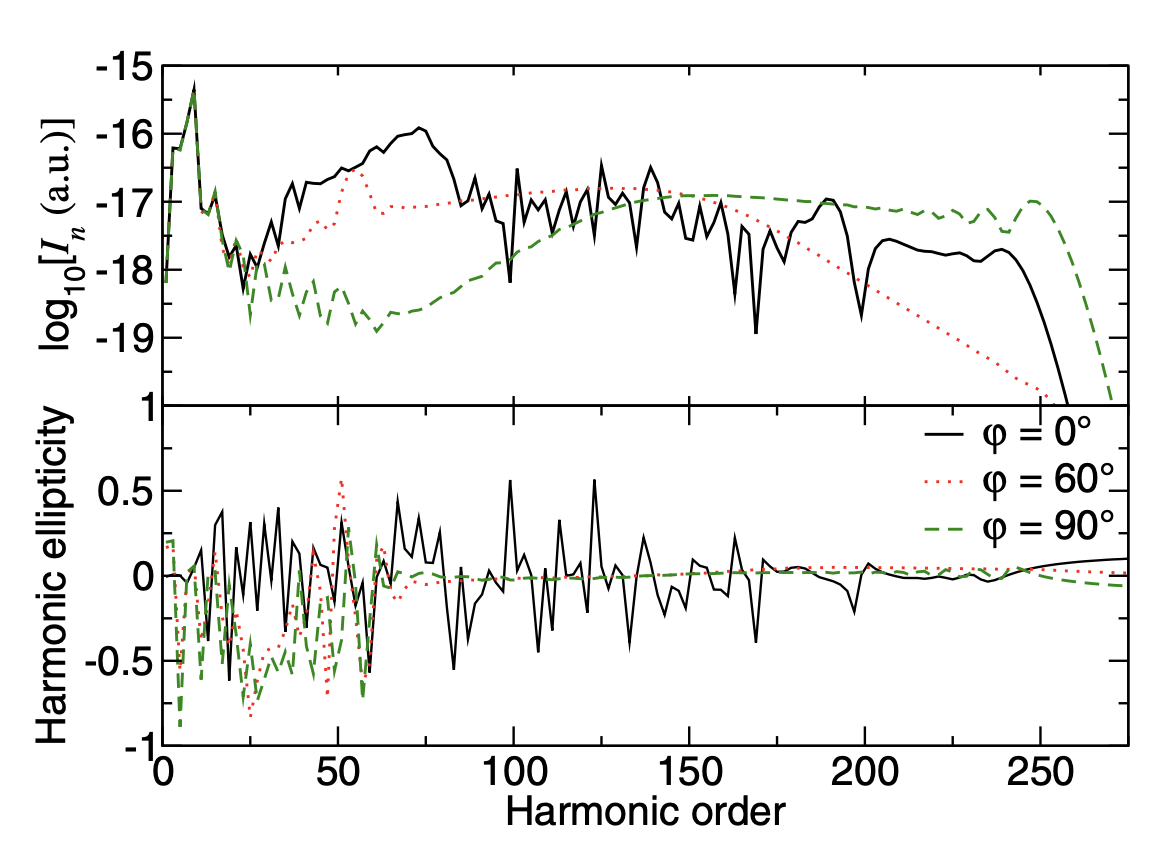
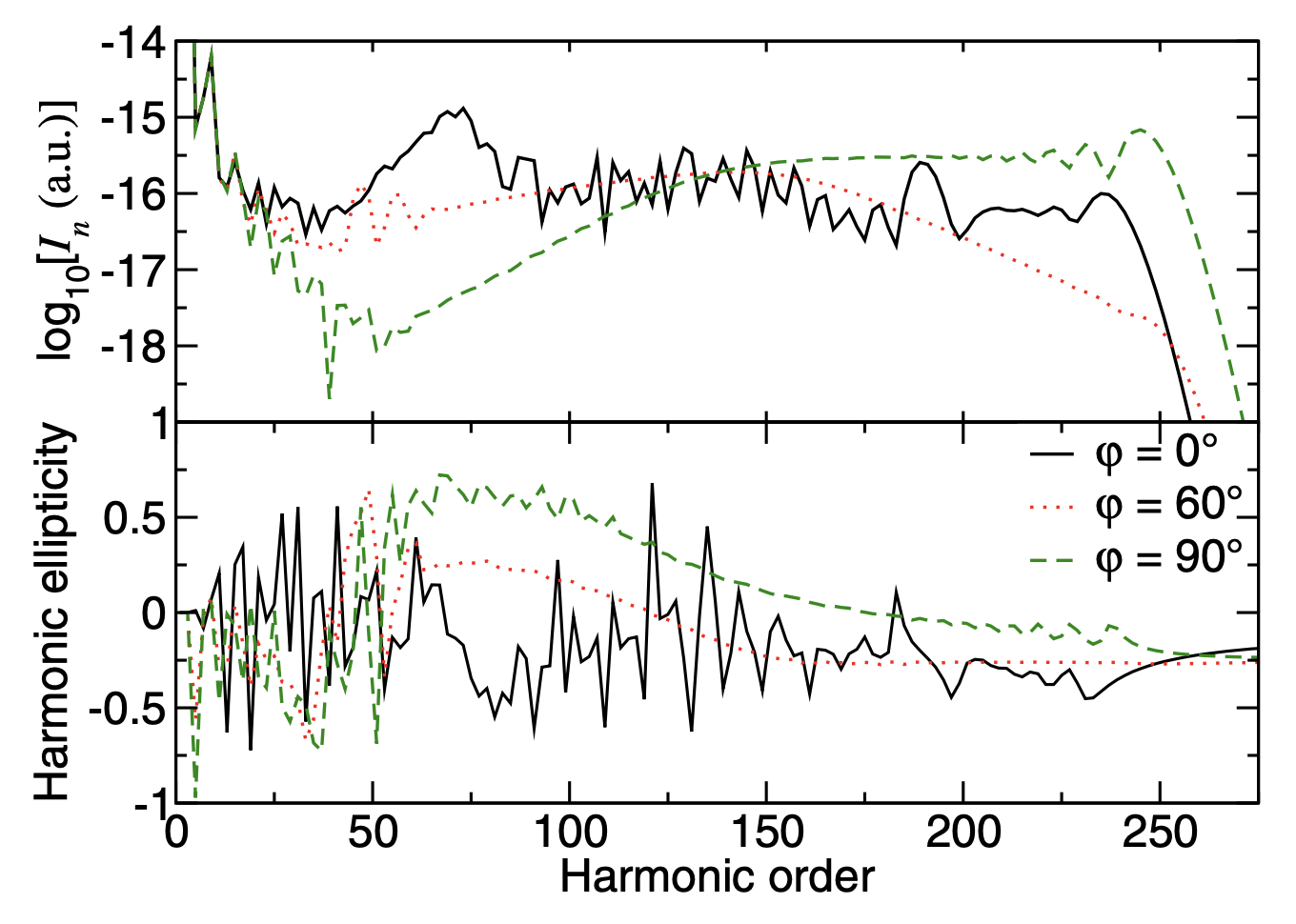
U ovom području elipticitet emitovanih harmonika je značajan, te se može generisati eliptički polarizovani atosekundni puls. Odgovarajući odnos R (gornji panel) kao i polarni dijagram električnog polja (donji panel) grupe od 26 uzastopnih harmonika počevši od harmonika n 59 su prikazani na slici ispod.

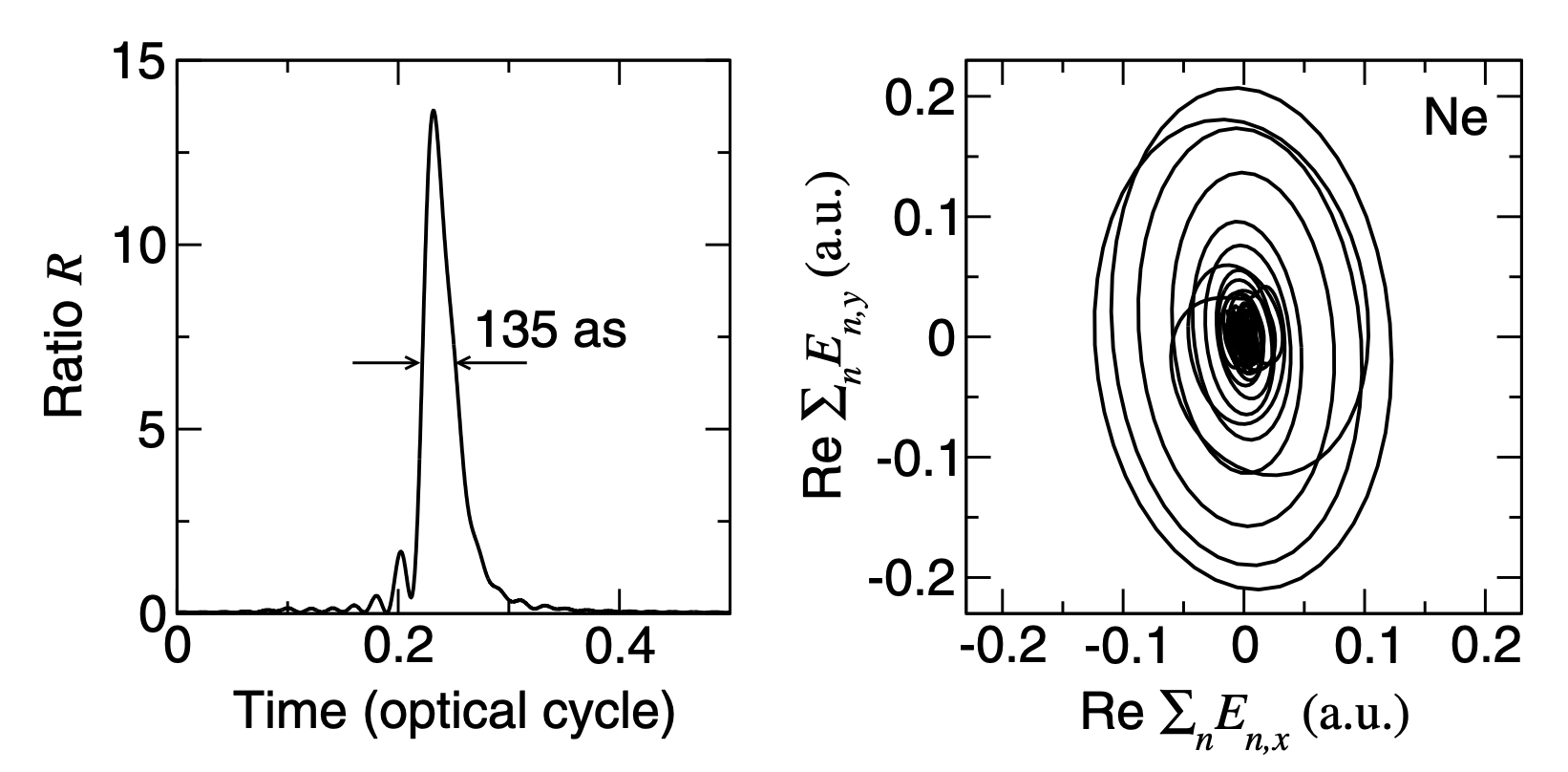
Širina generisanog atosekundnog pulsa se može kontrolisati pomoću relativne faze kao i izborom grupe viših harmonika. Pri tome je važno da odabrana grupa pripada glatkom dijelu spektra, tj. da su harmonici fazno-usaglašeni. Glatkoća spektra je objašnjena teorijom kvantnih orbita, dok se činjenica da je elipticitet harmonika generisanih sa neonom kao metom veći od elipticiteta harmonika generisanih izlaganjem atoma helijuma OTC polju objašnjava različitim osnovnim stanjem ovih atoma. Naime, atom helijuma ima s osnovno stanje kojem odgovara samo jedna vrijednost magnetnog kvantnog broja m (m = 0). Sa druge strane, neon ima p osnovno stanje kojem odgovara m=-1,0,1 . Stanje sa m = 0 ne doprinosi emisiji, ali stanja sa m=-1 i m=0  doprinose i njihovi doprinosi ukupnoj vjerovatnoći emisije su različiti. Dodatno, elipticiteti harmonika koji odgovaraju stanjima sa m=1 i m=-1 i su različiti. Ovo vodi do toga da za realno osnovno stanje, koje je superpozicija stanja sa m=1 i m=-1 , emitovani harmonici budu eliptički polarizovani sa značajnim elipticitetom. Naprimjer, intenzitet emisije (donje krive, lijeva osa) i elipticitet emitovanih harmonika (gornje krive, desna osa) kao funkcije reda harmonika su predstavljeni na donjoj slici za atom neona i OTC polje sa relativnom fazom . Očigledno je da je u jednom dijelu spektra doprinos stanja sa (n veći od 149), dok je situacija obrnuta za drugi dio spektra (n je između 49 i 149).

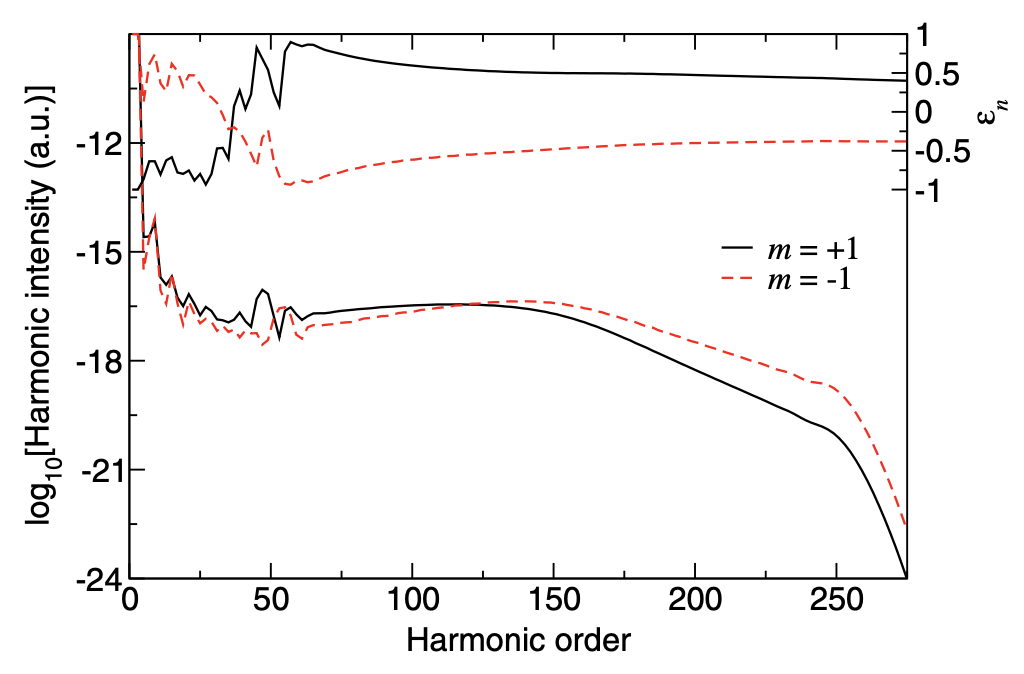
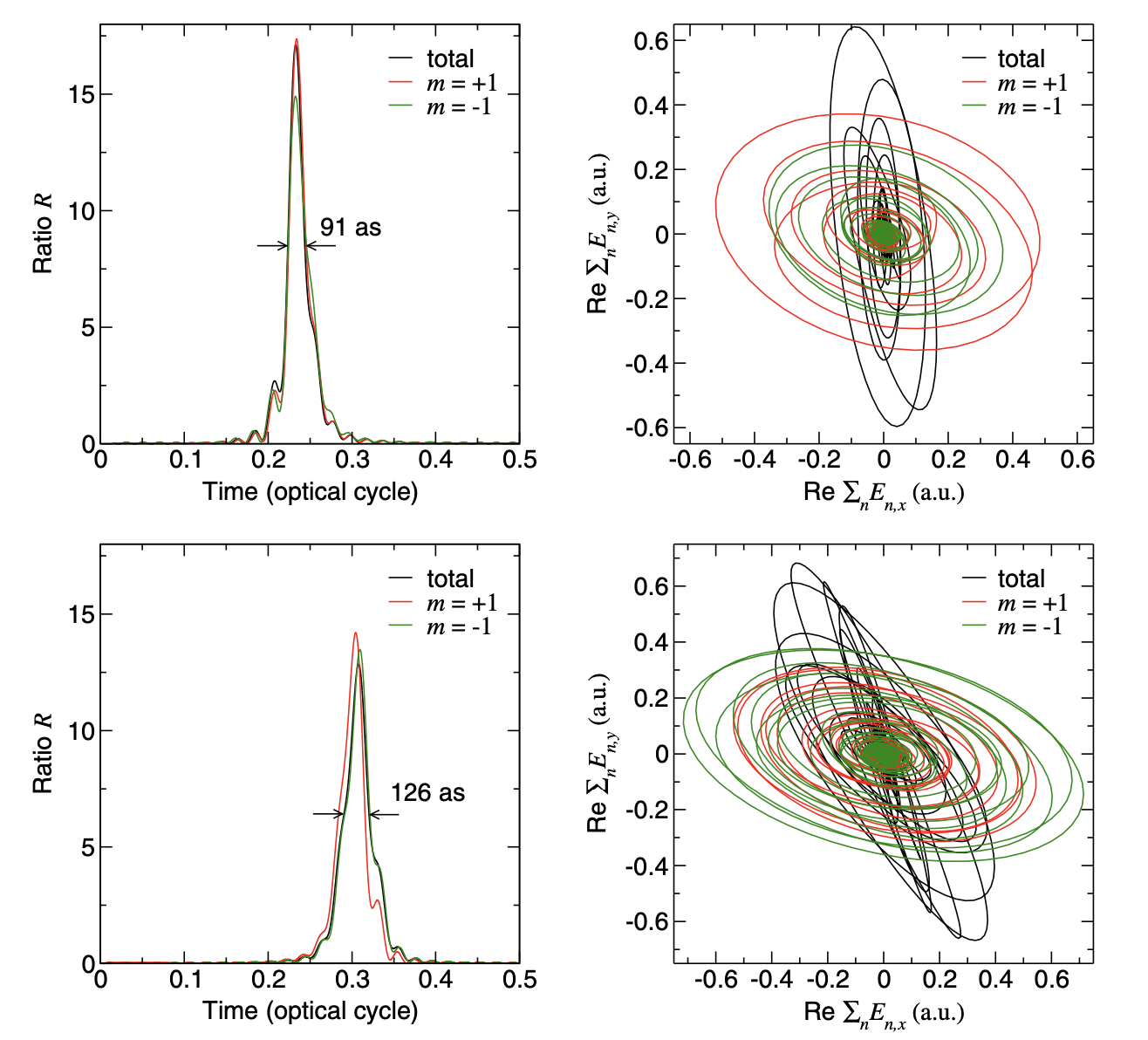
Kao posljedica, karakteristike odgovarajućih atosekundnih pulseva su različite. Gornji paneli slike ispod odgovaraju grupi od 26 harmonika počevši od harmonika n=59 , dok donji red odgovara ponovno grupi od 26 harmonika, ali sada sa početkom od n=125. U lijevoj koloni su predstavljene odgovarajuće vrijednosti odnosa R kako za realno osnovno stanje, tako i za stanja koja odgovaraju određenoj vrijednosti magnetnog kvantnog broja m. U desnoj koloni su predstavljeni odgovarajući polarni dijagrami rezultujućeg električnog polja.

Konačno, možemo zaključiti da se gore opisana šema može upotrijebiti za efikasnu generaciju eliptički polarizovanih atosekundnih pulseva ukoliko se kao meta koriste atomi sa p osnovnim stanjem. Elipticitet harmonika je povezan sa činjenicom da su doprinosi stanja koja odgovaraju različitim vrijednostima magnetnog kvantnog broja različiti. Elipticitet generisanog pulsa se može kontrolisati pomoću relativne faze kao i odabirom grupe harmonika za generaciju. Dodatno, približno kružno polarizovani puls je moguće generisati ukoliko se može ostvariti stanje sa dobro definisanom vrijednošću magnetnog kvantnog broja m. Važno je napomenuti da ideja iskorištena u ovom radu može biti proširena na druge kombinacije frekvencija komponenata laserskog polja. Takođe, ukoliko polarizacije komponenata laserskog polja nisu međusobno okomite, eliptički polarizovani harmonici se mogu očekivati nezavisno od frekvencija komponenata laserskog polja. Ovo je značajno jer omogućava korištenje eksperimentalno lakše dostupnog polja kod kojeg je frekvencija druge komponente dva puta veća od frekvencije prve. Na kraju, napomenimo da se i odnos intenziteta komponenata polja takođe može iskoristiti kao kontrolni parametar procesa.

• Prethodna
• Sljedeća