Youngov eksperiment sa elektronima

1.1 Šta je to klasično u vezi klasične fizike?

Sredinom 1920-tih francuski fizičar Lous de Broglie u svojoj doktorskoj disertaciji iznosi hipotezu da su elektroni dualne prirode: nekad pokazuju samo čestična svojstva kao što su masa, brzina, položaj, naelektrisanje i dr. , a nekad samo talasna svojstva. Njegova hipoteza bila je zasnovana na Einsteionovoj teoriji fotoefekta prema kojoj je elektromagnetno zračenje dualne prirode – nekad se ponaša čisto kao elektromagnetni talas, a nekad čisto kao snop čestica, tj. fotona. Ako elektromagnetno zračenje može da se nekad ponaša kao elektromagnetni talas, a nekad kao snop čestica, zašto onda čestice ne bi mogle da se ponašaju kao talasi? De Broglievo rezonovanje dovelo do razvoja nove fizikalne teorije, kvantne mehanike.

De Broglieva hipoteza je potvrđena u eksperimentima sa difrakcijom elektrona na kristalnoj rešetki. Detektovani elektroni na filmu su pokazali jasno uočene difrakcione maksimume, a znamo da su difrakcija i interferencija osobine talasa, kako zvučnih tako i elektromagnetnih talasa. Međutim, ako se elektron ponaša kao talas, a ne kao čestica, kako možemo znati gdje se elektron nalazi. Talas je pojava koja se širi prostorom i nema tačno određeni položaj. Iz iskustva znamo da ako bacimo kamen u vodu, nastaje vodeni talas koji se širi površinom vode. Ne možemo reći gdje se nalazi talas jer će s vremenom on zauzeti cijelu površinu vode. Iz ovog primjera se može vidjeti konceptulani problem u koji je zapala kvantna mehanika u svojim ranim godinama.

Prije nego se uhvatimo u koštac sa ovom centralnom temom kvantne mehanike, vratimo se na trenutak na klasičnu fiziku koja je zasnovana na Newtonovoj mehanici i Maxwellovoj teoriji elektromagnetizma. Šta je to što klasičnu fiziku čini klasičnom? Klasična fizika je zasnovana na tri principa: determinizam, neprekidnost i lokalnost.

Zakoni klasične fizike su zasnovani na diferencijalnim jednačinama koje se rješavaju poznavajući početne i granične uslove. Ovo se najbolje može razumijeti na primjeru kretanja nebeskih tijela. Ako poznajemo silu koja uzrokuje kretanje nekog nebeskog tijela (gravitaciona sila) i ako poznajemo gdje se tijelo nalazilo u nekom početnom trenutku posmatranja, onda na osnovu Newtonovog zakona možemo odrediti gdje će se tijelo nalaziti u bilo kojem budućem trenutku, pa čak i gdje se nalazilo u prošlosti. Na taj način astronomi su u mogućnosti da proračunaju kada nastupa pomračenje Sunca ili neki drugi astronomski događaj. Prema tome, poznavanjem sile i početnog položaja kao i početne brzine možemo u potpunosti odrediti (determinirati) kretanje tijela. Ovo je poznato kao Newton-Leibnizov princip determiniranosti.

Rješenja diferencijalnih jednačina moraju biti “glatke” funkcije, odnosno funkcije koje su neprekidne i dovoljno puta diferencijabilne u prostoru od interesa (princip neprekidnosti).

Princip lokalnosti podrazumijeva da se prenos sile odvija lokalno. Ovo znači da na tijelo djeluju samo tijela koja se nalaze u njegovoj neposrednoj blizini.

Sve tri ove karakteristike kvantna mehanika u potpunosti odbacuje. Za razliku od klasične fizike, kvantna mehanika je nedeterministička teorija koja je zasnovana na statističkoj interpretaciji. To podrazumijeva da ne možemo govoriti gdje se tačno elektron nalazi nego možemo govoriti samo o vjerovatnoći da se elektron nađe u određenom dijelu prostora. Štaviše, putanja kretanja gubi svaki smisao u mikrosvijetu jer talas ne može imati tačno određenu putanju, nego ih može biti beskonačno mnogo.

Međutim, postavlja se pitanje šta je to što eksperimentalci mjere. Da li je to vrijednost neke veličine ili nešto drugo. Razmotrimo sljedeći eksperiment. Rasijavamo elektrone na kristalnoj rešetki. Eksperimentalac detektuje elektron pod uglom od 40 stepeni u odnosu na kristal. Ako ponovimo isti eksperiment pod istim uslovima mogli bismo detektovati elektron pod nekim drugim uglom koji je različit od 40 stepeni. Kako to da isti eksperiment izveden pod istim uslovima daje različite rezultate? Razlog je jednostavan. Elektron je talas kao što smo već spomenuli. Ono što detektujemo u eksperimentu je samo jedan od mogućih ishoda eksperimenta. Koji će biti ishod eksperimenta mi to ne znamo sve do trenutka mjerenja. U ovome je suština je famozne Kopenhagenške interpretacije kvantne mehanike.

1.2 Youngov eksperiment sa elektronima

Konceptualni problem kvantne mehanike može se najbolje shvatiti na primjeru eksperimenta sa dvije pukotine (eng. Double–Slit Experiment) kojeg je prvi put izveo Thomas Young početkom 19. stoljeća u kojem je dobio interferentnu sliku svjetlosti i tako pokazao da je svjetlost talasne prirode, što je na kraju potvrđeno i Maxwellovom teorijom elektromagnetizma. Ni sam Young nije mogao naslutiti važnost ovog eksperimenta koji se i dan danas u različitim oblicima izvodi, o čemu ćemo kasnije više govoriti.

Čuveni fizičar druge polovine 20. stoljeća Richard Feynman za ovaj eksperiment kaže “cijela kvantna mehanika može biti posmatrana koristeći se razmišljanjima i posljedicama ovog jednog eksperimenta” [1] .

Razmotrimo kako se materija, odnosno snop klikera ponaša kada ih propustimo kroz jednu pukotinu i kroz dvije pukotine. Na donjim slikama se jasno vidi da klikeri prolazeći kroz pukotine ostavljaju likove pukotina na ekranu.

Slika 1. Prolazak klikera kroz jednu pukotinu. Na ekranu se vidi lik pukotine.

Slika 2. Prolazak klikera kroz dvije pukotine. Na ekranu se vide likovi obiju pukotina.

Pogledajmo sada šta se dešava sa vodenim talasima. Propuštanjem vodenog talasa kroz jednu pukotinu, na ekranu se pojavljuje jedna svijetla pruga koja slikovito predstavlja intenzitet talasa u datoj tački prostora. Što je pruga svjetlija, to je talas intenzivniji. Ovo je ista situacija koju smo imali kod klikera, tj. materije. Ovdje nema ništa čudno.

Ako propustimo vodene talase kroz obje pukotine istovremeno, dobijamo nešto sasvim novo – interferentnu sliku. Dva talasa prolazeći kroz pukotine, međusobno se slažu odnosno interferiraju, tako da u tačkama u kojima se susreću “brijeg” i “dolja” nestaje talas. Ova vrsta interferencije zove se destruktivna interferencija. Ako se u istoj tački susretnu dva “brijega” ili dvije “dolje” nastaje talas koji je intenzivniji od prethodna dva talasa. Ovakvu interferenciju zovemo konstruktivnom interferencijom.

Slika 3. Prolazak vodenog talasa kroz jednu pukotinu. Talas je najntenzivniji duž prave koja spaja ekran i pukotinu. Intenzitet talasa  je predstavljen svijetlom prugom.

Slika 4. Prolazak vodenog talasa kroz dvije pukotine istovremeno. Tačke u kojima se javljakonstruktivna interferencija predstavljene su  sa svijetlim prugama, a tačka u kojima je javlja destruktivna interferencija tamnim prugama.

Da zaključimo, talasi pokazuju interferenciju, a klikeri (materija) ne.

Pređimo sada na mikrosvijet, svijet atoma, molekula, elektrona i drugih atomskih čestica. Šta možemo očekivati ako kroz pukotine propustimo elektrone? Ako je elektron čestica kao što su klikeri, onda očekujemo da prilikom prolaska kroz dvije pukotine dobijemo likove pukotina na ekranu.

Sve do 1960-tih, ovo je bio jedan od čuvenih misaonih eksperimenata kvantne mehanike jer nije postojala tehnička mogućnost da se provjeri njegova ispravnost. Claus Jönsson je u svom, sada već legendarnom radu, iz 1961. godine [2] pokazao da elektroni ipak pokazuju inteferenciju ako se propuste kroz dvije pukotine. Ovaj čuveni eksperiment sa elektronima je zapravo ništa drugo nego verzija Youngovog eksperimenta sa svjetlosnim talasima.

Eksperiment je 1974. godine ponovljen tako što je kroz dvije pukotine prolazio samo jedan elektron. I pored toga na filmu se mogle uočiti intereferentne pruge. Godine 1989. A. Tonomura [3] je koristeći preciznu tehnologiju za mjerenje dobio jasnu sliku interferencije. Na donjim slikama su predstavljenje dobijene interferentne pruge.

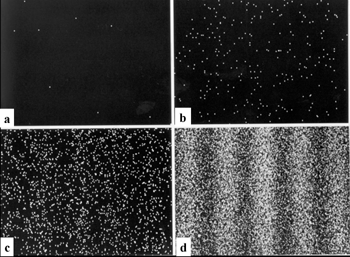
Slika 5. Interferencija elektrona na jednoj pukotini. Slika je dobijena za nekoliko različitih trenutaka posmatranja. Nakon dovoljno dugog vremena interferentne pruge se pojavljuju.

Ovi eksperimenti su nedvojbeno pokazali jednu veoma čudnu stvar. Elektron kao čestica putuje ka pukotinama, zatim postaje talas koji prolazeći kroz pukotine interferira sam sa sobom da bi konačno udario u ekran kao čestica. Matematički, još je čudnije. Postoji mogućnost da elektron prođe kroz samo jednu od dvije pukotine, ili da prođe kroz obje pukotine istovremeno, ili da ne prođe ni kroz jednu pukotinu. Sve ove mogućnosti međusobno se superponiraju (miješaju) dajući konačni rezultat.

U cilju utvrđivanja kroz koju pukotinu zaista elektron prolazi, postavljeni su detektori na mjestima pukotina. Međutim, kvantni svijet je čudniji nego što smo ikad mogli zamisliti. Mjerenja su pokazala da elektron prolazi samo kroz jednu pukotinu, a ne kroz dvije kao što teorija predviđa. Sam čin mjerenja značio je da se elektron ponaša kao čestica, a ne kao talas. Kao da je elektron bio svjestan da ga se posmatra pa je odlučio da se ponaša drugačije. Ova činjenica je u skladu sa već spomenutom Kopenhagenškom interpretacijom kvantne mehanike: ne znamo kroz koju pukotinu elektron prolazi sve dok ne izmjerimo.

Čitatelji PhysicsWorld.com su 2002. godine proglasili Jönssonov eksperiment sa elektronima najljepšim ikad izvedenim eksperimentom u fizici [4].

Međutim, priča sa double-slit eksperimentom ne prestaje ovdje. Grupa naučnika među kojima je i prof. dr. Dejan Milošević sa Prirodno-matematičkog fakulteta Univerziteta u Sarajevu objavili su rad 2005. godine u renomiranom svjetskom časopisu Physical Review Letters [5] u kojem su prvi put predstavljene inteferentne pruge elektrona koji prolaze ne kroz pukotine u prostoru kao u Jönssonovom eksperimentu nego kroz “pukotine” u vremenu.

U klasičnom Youngovom eksperimentu pruge se formiraju kada svjetlost prolazi kroz dvije pukotine. Ako svjetlost prolazi kroz jednu pukotinu inteferentne pruge se ne opažaju.

U vremenskoj verziji double-slit eksperimenta korišten je laserski puls koji se imao dva maksimuma i jedan minimum (maksimum u suprotnom smjeru). Detektori su postavljeni na suprotnim strana (Slika 6). Samo u trenutku kada lasersko polje postiže maksimalnu vrijednost postoji značajna vjerovatnoća da će se atom jonizovati. To znači da maksimum laserskog polja otvara tzv. “prozor u vremenu” kroz koji elektron može da napusti atom.

U slučaju kada imamo samo jedan “prozor u vremenu” sa velikom sigurnošću možemo tvrditi kada je došlo do jonizacije atoma. Međutim, u slučaju kada imamo dva maksimuma laserskog polja, odnosno dva “prozora u vremenu”, onda elektron može da napusti atom kroz bilo koja od ova dva prozora. S obzirom da ovi prozori imaju ulogu Youngovih pukotina dolazi do efekta interferencije elektronskog talasa koji se opaža samo kada se energija detektovanih elektrona predstavi u zavisnosti od vremena, odnosno faze laserskog polja. Razlog tome je činjenica da “pukotine” nisu u prostoru kao u Jönssonovom eksperimentu nego u vremenu.

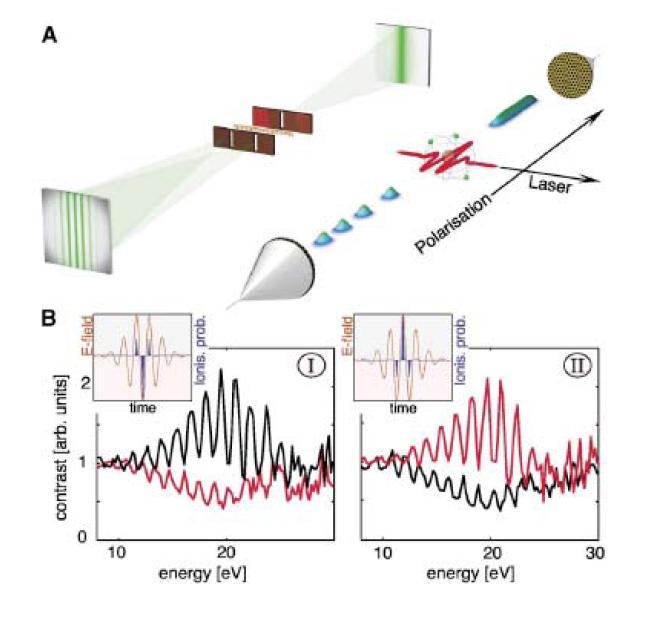
Slika 6. Eksperimentalna postavka double-slit eksperimenta u vremenu. Lijevi detektor registruje elektrone koje se jonizuju u trenutku kada laserski puls ima maksimum, dok desni detektor registruje elektrone koji se jonizuju u trenutku kada laserski puls prolazi kroz maksimum u suptronom smjeru.

Slika 7.Zavisnost energije detektovnih elektrona od vremena. Na desnom detektoru jasno su izražene interferentne pruge nastale interferencijom elektronskog talasa koji može da napusti atoma kroz dva “prozora u vremenu”.

Na slici 6. je predstavljena eksperimentalna postavka. Desni detektor registruje elektrone koji mogu da se jonizuju kroz dva prozora u vremenu dok lijevi detektor registruje elektrone koji se jonizuju kroz samo jedan prozor. Na lijevom detektoru nemamo inteferenciju jer imamo samo jednu “pukotinu”, dok u spektru elektrona na desnom detektoru možemo opaziti efekat interferencije. Na slici 7. je dat spektar ovih elektrona u zavisnosti od faze laserskog polja. Crvena boja predstavlja maksimume, a plava minimume interferencije. Na desnom detektoru jasno se mogu uočiti maksimumi i minimumi.

Međutm, priča oko intereferencije elektrona još uvijek nije završena.

U prethodne dvije godine u Japanu su izvedeni prvi HATI eksperimenti sa nasumično orijentisanim molekulama izloženim jakom laserskom polju [6]. U eksperimentu su detektovani HATI elektroni sa energetskom i ugaonom raspodjelom.Objasnimoukratko pojam HATI-ja. Skraćenica dolazi od engleskih riječi High-Order Above-Threshold Ionization, što bi u slobodnom prijevodu značilo jonizacija iznad praga višeg reda [7, 8]. Naime, pri izlaganju atomskih i molekularnih sistema jakom laserskom polju može nastati efekat jonizacije iznad praga (eng. Above-Threshold Ionization, ATI) [9]. U ovome procesu elektron apsorbuje mnogo više fotona nego što mu je potrebno za jonizaciju (prisjetimo se već famoznog fotoelektričnog efekta u kojemu elektron prima samo minimalan iznos energije potreban za bijeg iz metala). Pod uticajem laserskog polja, jonizovani elektron može biti vraćen u blizinu matičnog atomskog (molekularnog) jona, na njemu se rasijati, te nakon toga poprimiti dodatnu energiju prije nego stigne do detektora. Ovi elektroni se nazivaju HATI elektroni ili visokoenergetski elektroni. U navedenim eksperimentima su korištene dvoatomske molekule, konkretno N2 i O2 , koje su karakterisane različitom simetrijom što je od krucijalne važnosti za objašnjenje rezultata ovog eksperimenta.

Emisija elektrona sa dvoatomskih molekula je konceptualno slična originalnom Jönssonovom eksperimentu. Lasersko polje može da jonizuje prvi atom molekule. Slobodni elektron koji je pri tome nastao može da se rasije na svom matičnom atomu ili da se rasije na drugom atomu dvoatomske molekule. Također postoji mogućnost da lasersko polje jonizuje drugi atom molekule, pri čemu slobodni elektron može da se rasije na svom matičnom atomu ili da se rasije na prvom atomu molekule. Kvantnomehanički sve ove mogućnosti međusobno se superponiraju dajući spektar kao što je prikazan na slici 8 i slici 9.

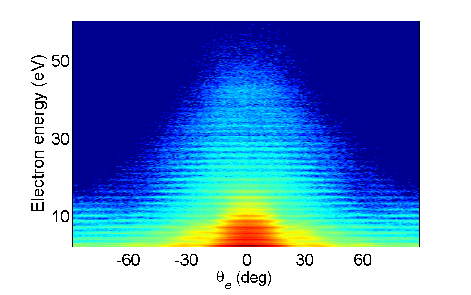
Slika 8. Eksperimentalno izmjereni spektar elektrona u zavisnosti od ugla detekcije.

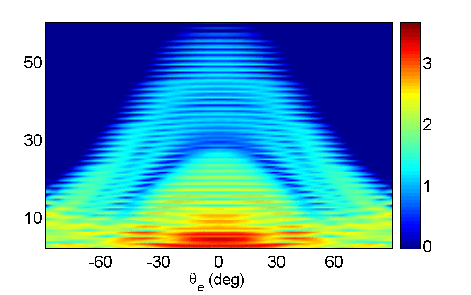
Slika 9. Teorijski proračauni. Iako nemamo idealno slaganje eksperimenta i teorije ipak teorija može  kvalitativno objasniti eksperimentalna mjerenja.

I nakon svega izloženog možemo zaključiti da i pored toga što je prošlo više od 200 godina od prvobitnog Youngovog eksperimenta sa svjetlosnim talasima, efekat interferencije koji je opažen u navedenim eksperimentima i dan danas ima važnu ulogu u kvantnoj fizici.

Reference:

[1] Brian Green, The Elegant Universe: Superstrings, Hidden Dimensions and the Quest for the Ultimate Theory, W.W. Norton. str . 97–100 (1999).

[2] C. Jönsson, Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten, Zs. Phys. 161, 454 (1961).

[3] A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki, H. Ezawa, Demonstration of single-electron buildup of an interference pattern, Am. J. Phys. 57, 117 (1989).

[4] http://physicsworld.com/cws/article/print/9746

[5] F. Lindner, M. G. Schätzel, H. Walther, A. Baltuška, E. Goulielmakis, F. Krausz, D. B. Milošević, D. Bauer, W. Becker, and G. G. Paulus, Attosecond Double – Slit Experiment, Phys. Rev. Lett. 95, 040401 (2005).

[6] M. Okunishi, R. Itaya, K. Shimada, G. Prümper, K. Ueda, M. Busuladžić, A. Gazibegović-Busuladžić, D. B. Milošević, and W. Becker, Two-Source Double-Slit Interference in Angle-Resolved High-Energy Above-Threshold Ionization Spectra of Diatoms, Phys. Rev. Lett. 103, 043001 (2009).

[7] G. G. Paulus, W. Nicklich, H. Xu, P. Lambropoulos, and H. Walther, Plateau in Above-Threshold Ionization Spectra, Phys. Rev. Lett. 72, 2851 (1994).

[8] D. B. Milošević, Strong-Field Approximation for Ionization of a Diatomic Molecule by a Strong Laser Field, Phys. Rev. A 74, 063404 (2006)

[9] P. Agostini, F. Fabre, G. Mainfray, G. Petite, and N. K. Rahman, Free-free Transitions Following Six Photon Ionization of Xenon Atoms, Phys. Rev. Lett. 42, 1127 (1979).

• Sljedeća